信号的采样和分析是现代通信及信号处理的重要环节。使用ADC(模数转换器)对模拟信号进行数字化采样，将模拟信号转换为数字信号。从而方便数字信号处理、传输和存储。本文将实例介绍信号采样的过程，分析信号采样过程中可能会出现的问题，以便帮助工程师们进行采集数据的分析。

实例1、信号与采样的关联

若被采集信号为频率10kHz的正弦波。

当采样率为200Ksps时，一个信号周期采集20个样本。将采集的样本进行线性拟合。能够100%拟合为正弦波形。

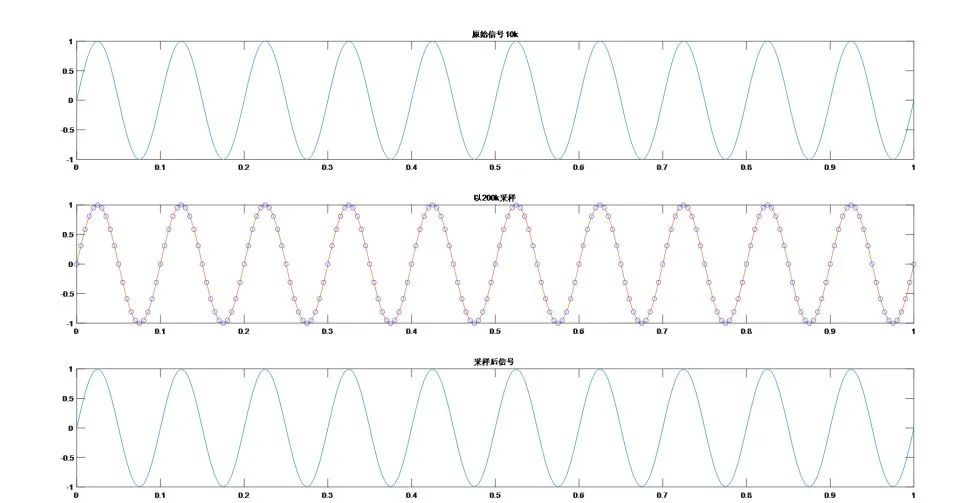 （图一）

当采样率为100Ksps时，一个信号周期采集10个样本。将采集的样本进行线性拟合。拟合后的正弦波形出现略微变形。

、

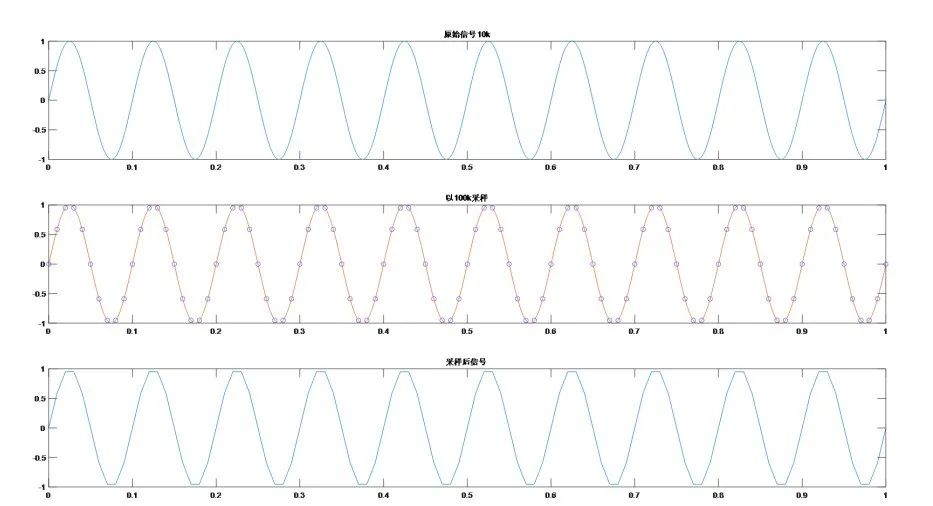
（图二）

当采样率为25Ksps时，一个信号周期采集2.5个样本。将采集的样本进行线性拟合。拟合后的波形变形严重，已无法识别出正弦信号波形。

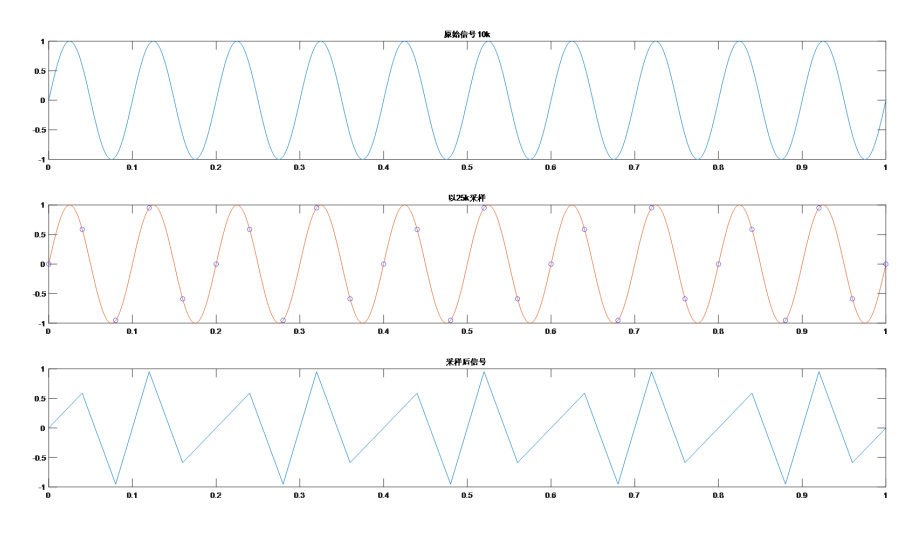（图三）

当采样率为信号频率的2.5倍时，拟合后的波形已无法还原为正弦波形，那么我们的采样率与信号频率到底应该满足什么样的关系呢？

采样率是指每秒钟对信号进行采样的次数。从上图实例中可以看出，采样率越高，能够采集到原始信号的更多细节。但并不是采样率越高越好，因为采样率过高也会带来一些难题。

高采样率会增加存储和处理信号的数据量，对系统资源要求更高。因此，在实际应用中，需要综合考虑信号特性、应用需求和系统资源来选择合适的采样率。

根据奈奎斯特采样定理，如果信号的最高频率是fx，则采样率需要大于等于2*fx。但上图三所示，在满足采样定理的条件下，依然无法拟合出正弦波形，这是否就意味着采样率设计不符合要求？答案：并不是。

如果在采样率满足采样定理的情况下，即使线性拟合出的波形不是正弦波形，也可以通过插值拟合还原出原始波形。如图，当被采集信号为频率10kHz的正弦波时，以采样率为25Ksps进行采样，采样之后通过插值拟合还原原始波形，可看出时域波形与原始信号波形一致。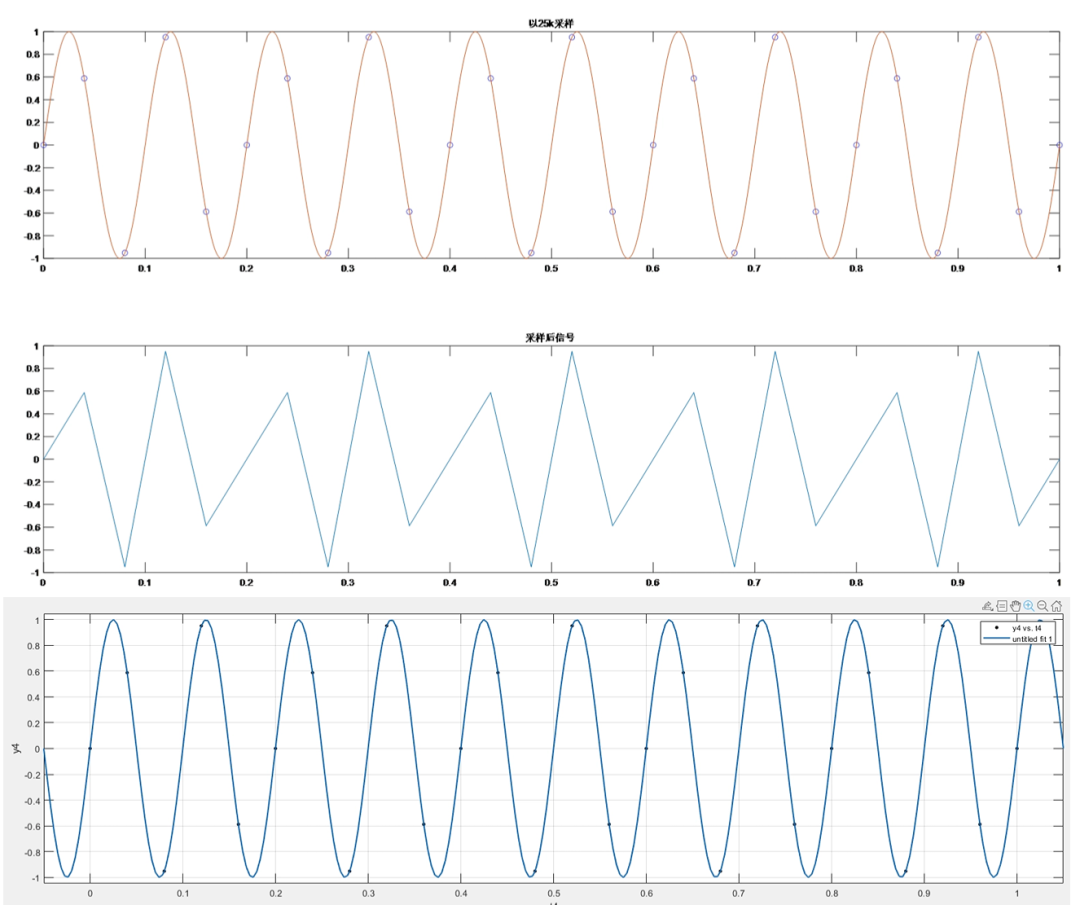        

（图4）

二、数字信号在时域和频域的表现

时域分析和频域分析是数字信号处理时常用的分析方式。

时域反映的是信号在时间轴上的变化情况。通过时域分析，我们可以获得信号的周期性、波形变化和幅度变化等信息。

时域通过数学方式变换得到频域。频域反应了信号在频率方面的特性。在频域中，信号被表示为不同频率成分和对应的幅度。频域表示了信号的频谱分布、频率成分和能量分布等信息。通过频域分析，我们可以了解到信号的频率成分、频率范围等。

综上所述，时域描述了信号在时间上的变化，频域描述了信号在频率上的特性，它们共同帮助我们理解和处理不同类型的信号。

上文实例一中采样的正弦波信号就是在时域展现的，除此之外，我们还可以通过频域观察采集到的信号。

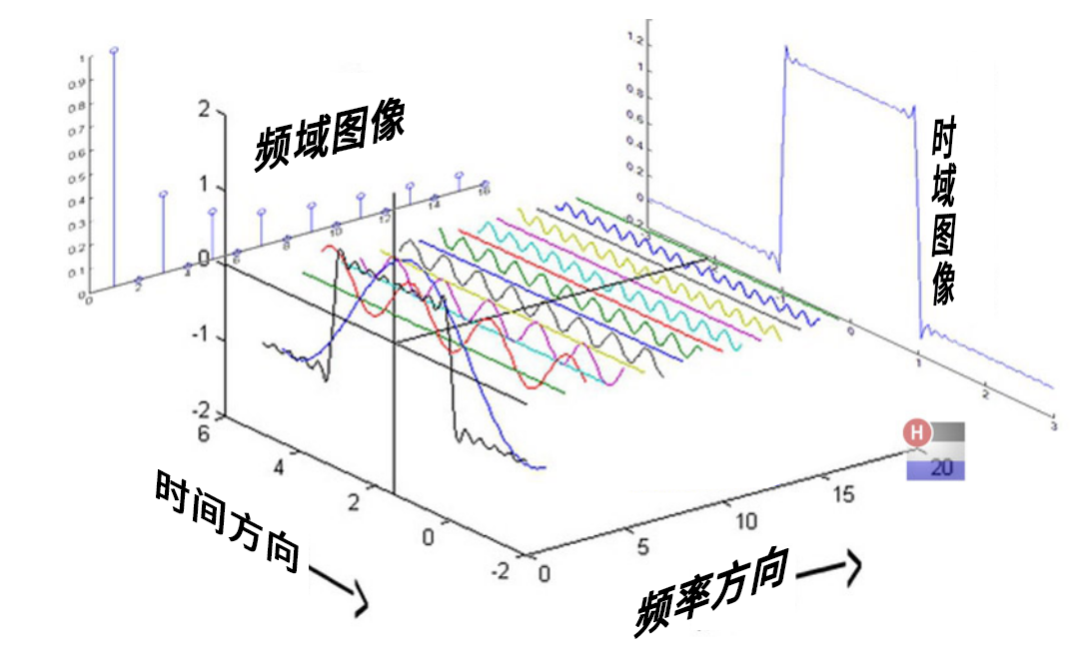
（图5，来源于微博 : @花生油工人）

时域和频域可以简单理解为是在不同的方向观察信号。下图所示就是一个方波信号在频域呈现的样子。

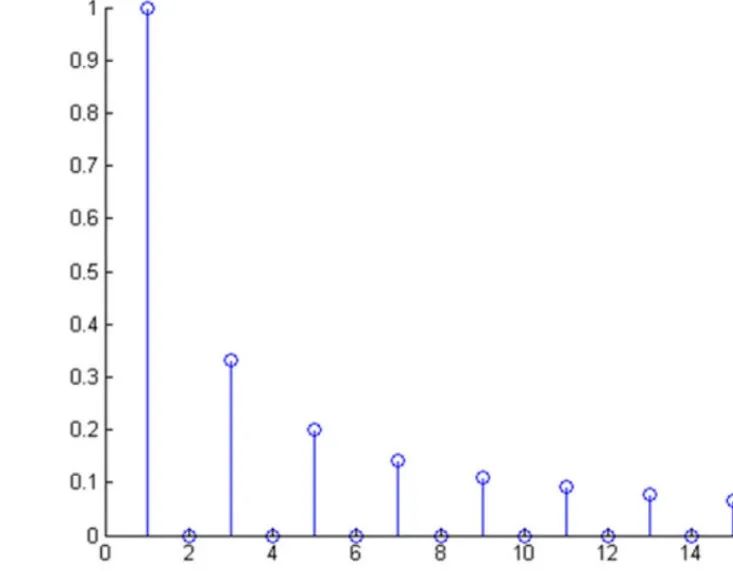
（图6，来源于微博 : @花生油工人）

时域和频域是相互关联的，在信号处理中经常需要在时域和频域之间进行转换。如果需要将采集到的信号从时域转到频域，需要对信号进行傅里叶变换。我们一般借助工具（如matlab、cooledit等 ）对采集到的信号进行做FFT（快速傅里叶变换）。然后取其幅度谱或功率谱就可以看到信号在频域上的展现。

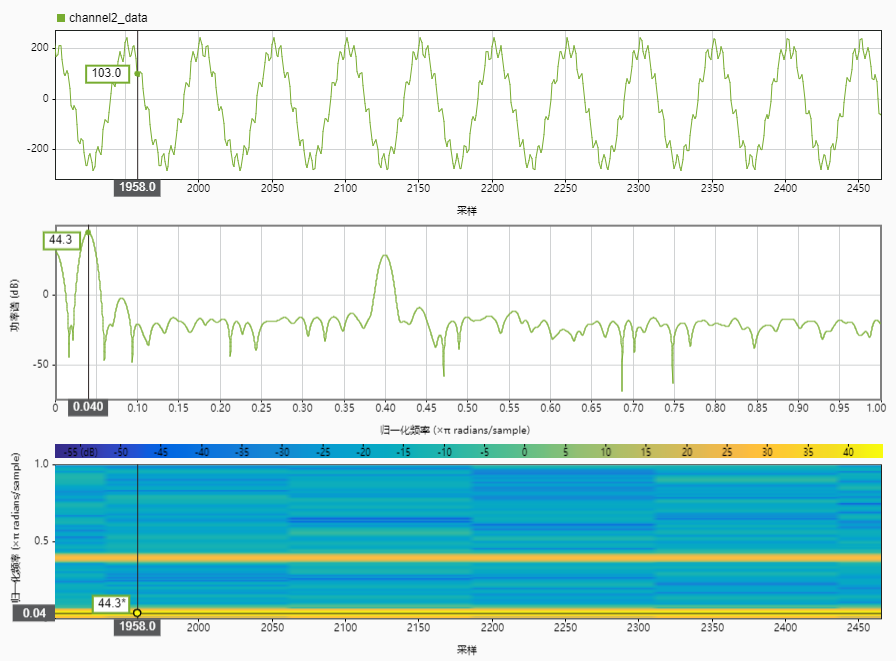
（图7）

三、频谱混叠现象

由于数字信号处理受到采样率的限制，必须要注意频谱混叠的情况。频谱混叠是由于频谱折叠导致的。那么什么是频谱折叠？什么是频谱混叠？

1、频谱折叠

若采样率为Fs，那么我们频域横轴代表的是信号频率，纵轴代表信号幅值。上图中横轴的最左边和最右边分别对应的就是0频点和Fs/2的频率点。

在信号频率不断增大时，纵轴表示频点的线就会不断的往右边移，当移到最右边也就是Fs/2处，它就会开始往回走，当采集的信号不断的增大时，在采样率的限制下就会不断的“折叠”。

2、频谱混叠

假设FS/2为100MHz，当信号走到9/10处时，就是90MHz，当信号为110MHz时，由于频谱折叠，信号折叠回来又在9/10处。这个时候我们就分不清它到底是90MHz还是100MHz了。这就是频谱混叠的现象。

为了避免出现频谱混叠，造成无法分辨信号的情况，因此需要满足采样率大于等于2*信号频率的条件。

说到这里，我们不得不提到带通采样，什么是带通采样？

如上文频谱混叠中的例子所述，我们无法分辨在频谱9/10处的信号是90MHz还是110MHz？亦或是更高的频谱折叠回来的信号。那么假设已知被测信号的频率范围呢？

比如被测信号范围是105MHZ~115MH。我们就可以确定这个9/10处频率是110MHz。按照以上逻辑，采样率为200Msps时，可以采集频率为110MHz的信号，这个就可以理解为带通采样。只要被测信号的带宽小于FS/2，即可满足带通采样的条件。